Sandwiches

You know what a sandwich is right ? Stuff between 2 layers of bread, something like that. I thought I knew what sandwiches were too. But it was before I encountered this monstruosity:

credits: see wikipedia

A Toast Sandwich. A fu*ing Toast Sandwich. A piece of bread between 2 pieces of bread. At this point in time, the entire universe collapsed around me. What even is a sandwich ? Is toast itself a sandwich ? Is a Toast Sandwich a Sandwich Sandwich ? If you stack 2 layers of bread one on top of the other, is it a Nothing Sandwich ? I'm becoming insane, this is clearly not a sandwich. We have to ban it for the name of sanity.

No, wait a second. It must be a sandwich 😨. And I think I can prove it
- Axiom 1. We assume that if ||(X||) is a sandwich, ||(X||) with half as much filling is a sandwich. By induction, for any ||(n||), a sandwich with ||(2^{-n}||) as much filling is a sandwich.
- Axiom 2. We assume that sandwiches exist. This is a non-obvious fact, but this implies that they are made of atoms. In particular, the filling is made up of a finite number of atoms.
- Axiom 3. There is at least one person on earth that know what a sandwich is, and this person is not a scientist.
- Axiom 4. A hamburger is a sandwich. This fact is trivial.
- By 1) and 2), a sandwich with one atom of filling is a sandwich.
- But then by 3), the person who knows what a sandwich is can't make the difference between this sandwich and a sandwich without filling. We just proved an important theorem: a sandwich without filling is still a sandwich
- By 4, we know that this is a sandwich. Let's call it ||(S_3||):
- By our previous theorem, a ||(S_3||) without feeling is a sandwich.
- But this is equivalent (in a strong sense) to a Toast Sandwich.
Now I am become Death, the Destroyer of Worlds**

We have to do something then. We have to classify sandwiches once and for all.

The State of Research

This research is one of the uttermost importance. Generations of researcher have debated on the subject, and we only start to see the premises of a universal classification. ⚠️ This can be a very emotional and polarizing subject, so beware.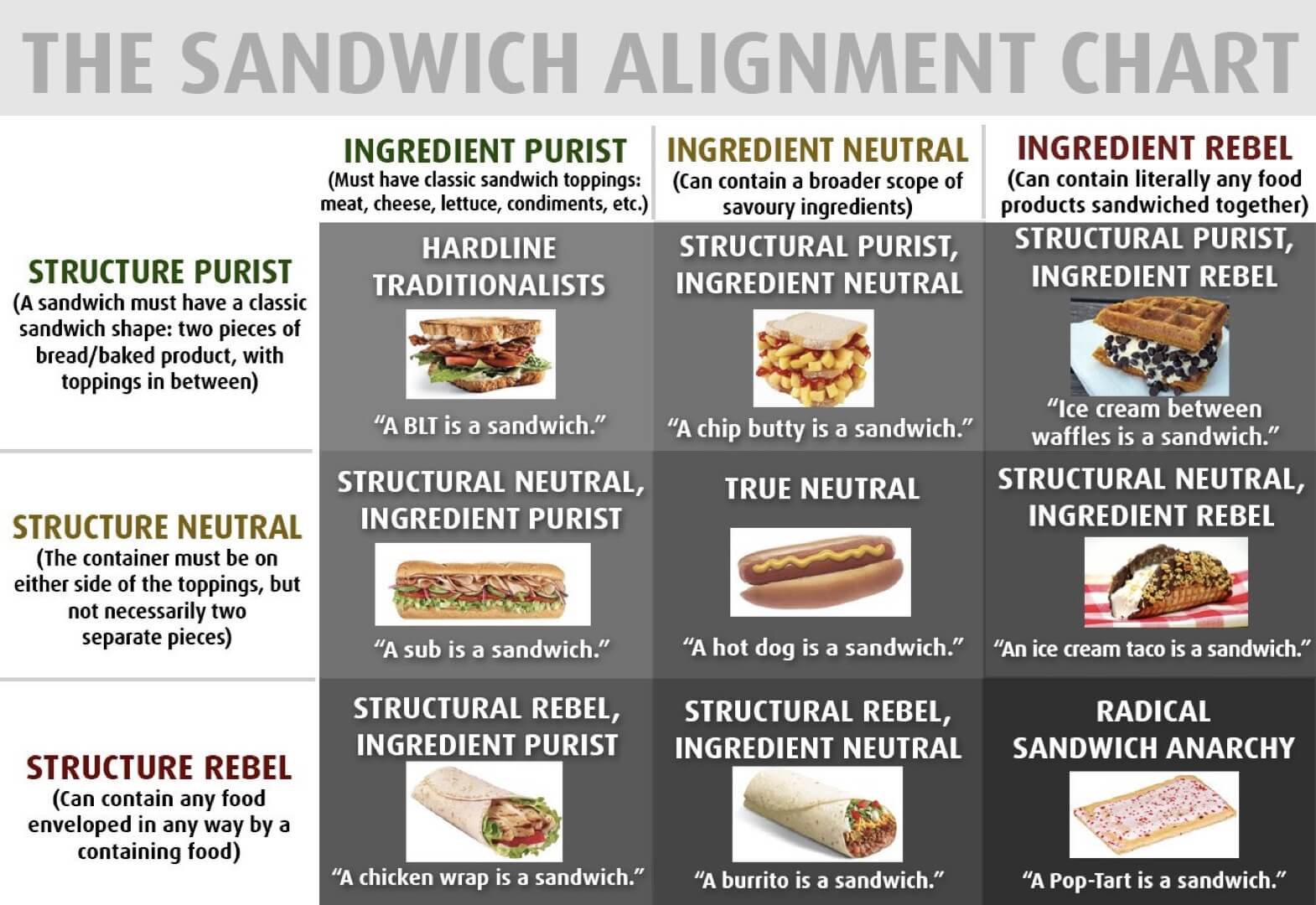

-

Definitions

Before I present the main theories, we need some definitions.

structural starch is anything made up mostly of long chains of glucose, and that can be hold in one hand.
What we will refer to as salad is anything that is edible and that is not structural starch. (that's actually a simplification because of Soup, but the theory would be too complex to explain here)
Crust is structural starch that can in theory hold salad. When it's the case, the salad is referred to as "the filling*.
Structural starch that cannot hold salad is quite rare, but does exist. We call them candies. For example, a ripped-off pancake is a candy.
Crust with salad does not automatically constitute a sandwich, but a proto-sandwich.

To make sure you understood, here are some basic questions:

Is rice structural starch, candy or salad ?
Salad. You can't hold rice in your hands. The only exception is sushi, when rice becomes Crust. In any case, rice is never candy.
Is lettuce salad ?
No: that's Crust. lettuce is made up of Cellulose, very long chains of glucose. And you can hold food with a leaf of lettuce. Here is the proof:
What is a potato ?
Many forms of potato exist, and it can be any of the 4. A single Potato is Crust. A Potato chip is Crust. And french fries are salad, because you never it a french frie alone (otherwise it would be a candy). Lastly, Aligot is a Candy, since you can hold it in your hand but you can't fill it with salad. Thus, potatoes are universal.

Theories

The structural approach

The last successful theory was the Cube rule. It is simple, often consistent, and almost purely topolical. Unfortunately, the approach still has a number of problems.

First and foremost, an uncut "Subway sandwich" is not a sandwich but a taco. That means that you can accidentally turn a non-sandwich into a sandwich, which makes the theory unstable.
Second, a non sandwich (a Taco) can be transformed continuously into a 1-Toast (a flat Taco), which makes the definition non-continuous.
a Big Mac is a cake ! WTF ? It completely breaks our intuition.
The Toast Sandwich cannot be classified with this theory, so the theory is non-universal

The topological approach

We can modify slightly the cube rule to use homology classes. To classify a sandwich, you just have to:

1) count the number of pieces of structural starch (or Toasts)
3) count the maximum number of 3-dimensional holes in your sandwich Toasts (if any)
2) count the maximum number of 2-dimensional holes in your sandwich Toasts (if any)

So, let's see some examples:

Name	Classification	Notes
Classical sandwich	\|\|(2\|\|)-sandwich	trivial
Crèpe bretonne	\|\|(1\|\|)-sandwich	obvious
Taco	\|\|(1\|\|)-sandwich	can be unfolded to get a pancake
Calzone	\|\|(1,1\|\|)-sandwich	0 holes in the surface, but a 3d hole inside
Rolled wrap	\|\|(1,0,1\|\|)-sandwich	homeomorphic to a pancake with a hole
Bretzel Sandwich	\|\|(2,0,3\|\|)-sandwich	2 slices of bread, that each have 3 holes

The main difference is that Quiches, Toast and Taco are now in the same category, the class "1-sandwich".
But it starts to be interesting for more complex Toasts, like baghir (same apply for bubble-wafles):

Name	Classification	Notes
Baghir	\|\|(1,\omega\|\|)-sandwich	Uncountably many 3d-holes
Big M'aghir	\|\|(3,\omega\|\|)-sandwich	The baghir version of a Big Mac
Rolled Baghir wrap	\|\|(1,\omega,1\|\|)-sandwich	a lot of holes

The geometrical approach

As we saw, the main problem with the topological approach is that it fails to distinguish a quiche from a toast. It is still unstable: if you take your calzone and cut an extremely small part just to check it's good, you know have a 1-sandwich. We need a way to have a theory that is less unstable, while not failing to identify in-between sandwiches (what if I put guacamole on a curved chip ?) For this reason, I and some colleagues developed T.O.A.S.T, Topological Outline Analysis of Sandwich Tangents

(The name was partially found by Claude 4.5 Sonnet, credits to it)

The idea is both simple and revolutionnary.

1) take your differentiable proto-sandwich (it's ok if it's not differentiable for a set of points of measure 0, just ignore them)
2) look at all the points that are in contact with salad.
3) look at all the normalized tangent vector of these points.
4) Move the vectors back to the origin. You get a subset of ||(S_2||) (the sphere), called the core of the sandwich. And now, we can do topology ON THIS SPACE !

We will be interested in the following quantities:

The number of 0-dimensional components of the core, ||(C_0||)
The number of 1-dimensional components of the core, ||(C_1||)
The number of $2-dimensional components of the core, ||(C_2||)

The signature of the sandwich is defined as ||((C_0, C_1, C_2)||) Let's see a few examples:

For the toast, there is one single vector tangent to salad (denoted in blue), so the core is a single point on the sphere. Thus, its signature is ||((1, 0, 0)||)